服务案例

轴承转子系统作为旋转机械的关键组成部分,其运转稳定性决定了旋转机械工作的可靠性。而滑动轴承转子系统由于其柔性特点导致系统在运行过程中轴心位置不断变化,直接影响轴承转子系统运行的稳定性,特别是在高精密机床中,主轴系统的轴心位置是决定机床加工精度的重要因素。

不少学者基于轴心轨迹分析轴承转子系统的稳定性:基于往复压缩机活塞杆轴心轨迹的变化规律,提出了一种智能检测往复压缩机故障的方法,并通过试验对磨损和撞缸故障进行了验证,结果表明所提出的故障诊断模型能有效检测出这2种故障,并且可以准确预测故障的恶化。

上述研究主要通过理论方法计算轴承转子系统在各种运行工况下的轴心轨迹,并讨论了轴心轨迹在工程实践中的一些应用。文献给出了轴承转子系统轴心位置的表征方法,直接通过呈90°安装的位移传感器1和2的读数变化表征轴心位置;然而,该方法表征的轴心位置只是近似结果,本文在这一方法的基础上,提出了轴心位置的精确表征方法。

一、测量过程及误差说明

测量轴心位置的位移传感器安装位置如图1所示。首先,在主轴与轴承不重合处,确定一个位移传感器的安装平面,如图1a所示;在该平面上呈90°安装2个位移传感器,如图1b所示。当主轴与轴承同心时,传感器1和2的读数分别为a和b,取此时的圆心为坐标原点,即轴心坐标为(0,0)。在主轴转动过程中,轴心与轴承中心会产生一定的偏心距,轴心位置从O点偏移到O1点,此时传感器1和2的读数分别为a+Δx和b+Δy。文献[15]认为此时测量得到的主轴表面偏移量Δx和 Δy即为轴心的横纵坐标;然而,此时轴心的实际坐标是(Δx0, Δy0),两者并不严格相等。为解释原因,参考如图2所示的轴心位置几何关系对上述问题进行说明。

(a) 轴向安装位置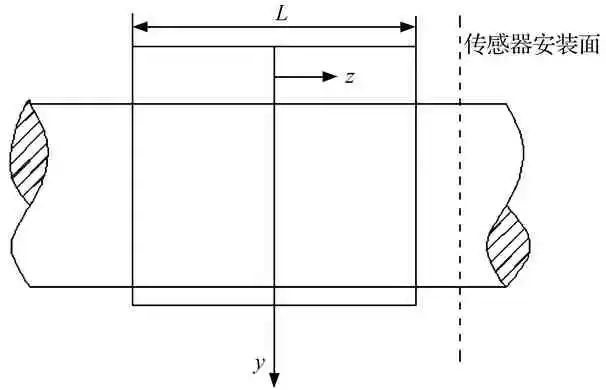

(b) 径向安装位置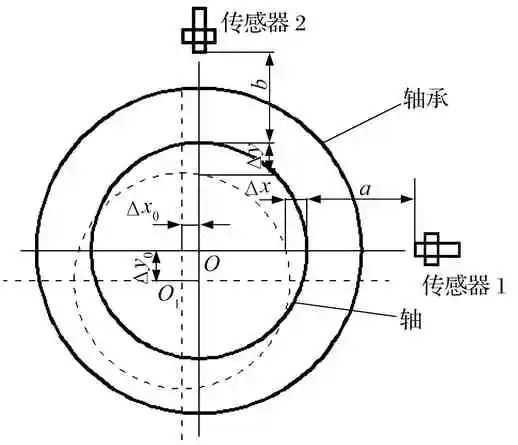

图2 轴心位置几何关系示意图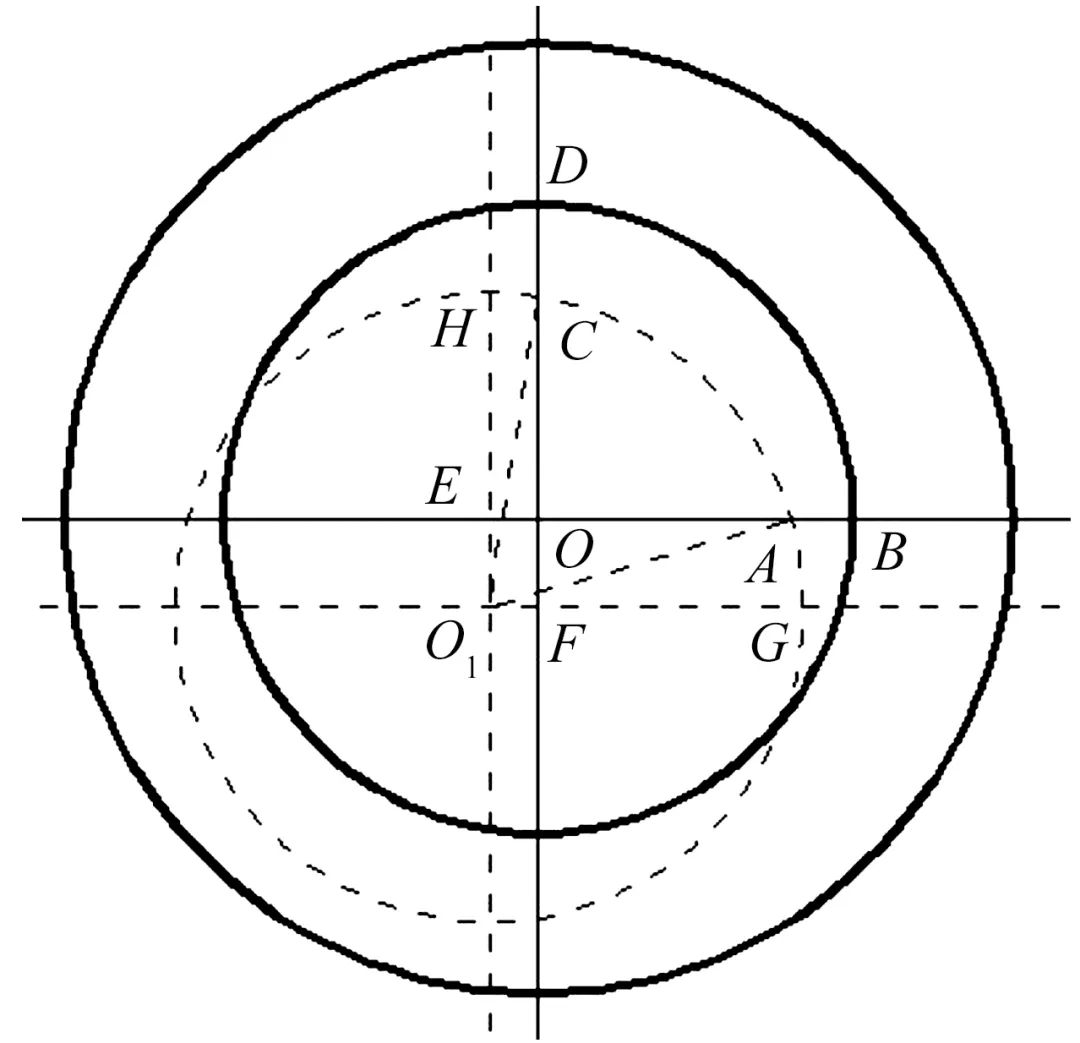

在Rt△O1EA和Rt△O1FC中,存在以下几何关系式

O1E2+EA2=O1A2=R2=OB2,

(1)

O1F2+FC2=O1C2=R2=OD2,

(2)

式中:R为轴半径。

结合图1和图2,存在如下对应关系式

O1F=Δx0,O1E=Δy0,AB=Δx,CD=Δy。

(3)

将(3)式代入(1)和(2)式并整理得

(4)

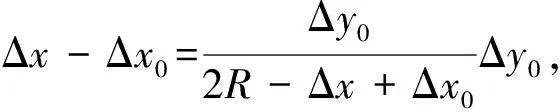
(5)

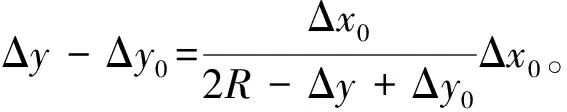
此时,若使用主轴表面偏移量(Δx,Δy)代替轴心的实际坐标(Δx0,Δy0),产生的相对误差为 

(6)

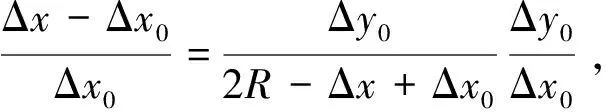
(7)

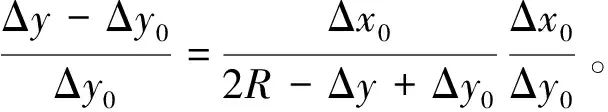
由(6)和(7)式可以看到,当轴心位置处于坐标轴附近时,即轴心的实际坐标(Δx0,Δy0)中有一个接近0时,用主轴表面偏移量(Δx,Δy)代替实际坐标(Δx0,Δy0)会产生明显的相对误差。因此,在表征高精密机床主轴的轴心位置时,不能直接通过主轴表面偏移量(Δx,Δy)代替实际坐标(Δx0,Δy0),即需要更精确的轴心位置表征方法。

二、 轴心位置的精确表征方法

对(4)和(5)式进行整理可得

(8)

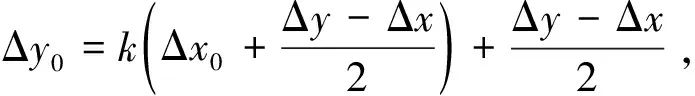
(9)

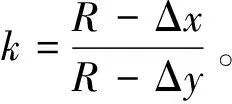
如图1中所示的滑动轴承转子系统,主轴半径R的量纲为毫米级,而主轴表面偏移量Δx和Δy的量纲为微米级,两者之间相差3个数量级,为避免实际测量过程中由于大数和小数的加减运算而产生截断误差,本文引入了参数k,由此得到轴心的实际坐标(Δx0,Δy0)可由参数k以及微米量级的Δx和Δy表示。

由(10)式可得,当Δx=Δy时,其表达式是无效的,为此需要在轴心处于Δx=Δy这一特殊位置时,给出轴心实际坐标的表达式。

当Δx=Δy时,由(8)式可得

Δy0=Δx0。

将(11)式代入(6)和(7)式,可得相对误差近似为

此时可以用(Δx,Δy)代替(Δx0,Δy0)表示轴心的实际位置。

综上所述,滑动轴承转子系统轴心位置的精确表征为:按照图1中的方式布置位移传感器,当传感器的测量值Δx与Δy相等时,轴心实际位置为Δx0=Δx,Δy0=Δy;当传感器的测量值Δx与Δy不相等时,轴心的实际坐标(Δx0,Δy0)由(8)—(10)式表征。

三、 算例

选择直径分别为20,50,100 mm的主轴,按照图1中的方式布置传感器,此时作如下设定:通过传感器测量得到这3种主轴表面的偏移量Δx=-1 μm,Δy=-45 μm。根据文献[15]中的表征方法,得到轴心坐标为(-1,-45)。按照本文所提新表征方法(8)—(10)式计算得到轴心纵坐标也是-45 μm,而横坐标存在较大差异,见表1。

计算结果显示,当轴心位置在y轴附近时,2种表征方法的纵坐标之间不存在差异,而横坐标之间存在明显的误差,并且主轴直径越小, 误差越明显。因此,当主轴位于图2中坐标轴附近的位置时,本文所提方法更能精确表征轴心位置。

表1 本文所提方法对轴心横坐标的表征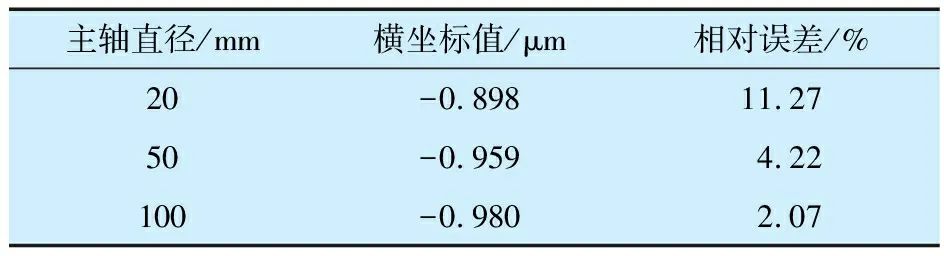

四、 结论

针对现有方法表征轴心位置存在误差的问题,在文献[15]的基础上提出了更精确表征轴心位置的方法。算例结果表明:当主轴表面偏移量Δx与Δy相等时,可以用Δx和Δy表征轴心实际位置(Δx0,Δy0),此时的相对误差在0.05%左右;当Δx与Δy不相等时,轴心实际位置(Δx0,Δy0)可由(8)和(10)式精确表征。

五、联系我们

让云科技-作为湖南地区知名品牌的工程轴承技术服务商及产品生产厂商，现已拥有两大自主品牌：让融（RANUR)、让云（RANUY )系列工程轴承，我们所做的一切只为时刻准备迎面解决更加严苛的运行工况及日益增长的市场需求，并及时掌握及应用如何提高产业可靠性及优化资产生命周期。

让融（RANUR)系列工程轴承是中国轴承高品质的保证，让融（RANUR)系列轴承拥有高精密的公差、设计独特的内部几何结构、高品质的工程轴承专用材料。

技术负责人电话：： 13657445999

销售负责人电话：： 13657443999

24小时官方电话：：4006-808-505

六、相关材料

不锈钢轴承	塑料轴承
绝缘轴承	陶瓷轴承